quarta-feira, 28 de setembro de 2016
terça-feira, 20 de setembro de 2016
sexta-feira, 30 de setembro de 2011
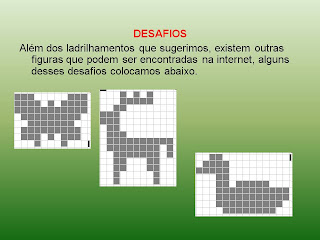
BRINCANDO COM PENTAMINÓS
POLIMINÓS
Os poliminós tem origem relacionada ao tradicional jogo "Tetris", conhecidíssimo daqueles que se utilizam do computador para diversões.Um pentaminó é um poliminó composto de cinco quadrados congruentes, conectados ortogonalmente.
Atentando para a forma, só existe um único tipo de dominó (dois "cubos" ou "quadrados" unidos por um dos lados). Se há um único tipo de dominó, existem dois tipos de triminós e cinco tipos de tetraminós. Já com os pentaminós o número pula a doze.
A proposta do pentaminós é a seguinte: cada peça é formada por 5 cubos, unidos pelos lados. O total são 12 peças diferentes, que permitem a criação de inúmeros problemas e suas soluções.
Para melhor entendimento, costuma-se nomear as peças pelas letras do alfabeto com as quais elas se parecem.
 As doze peças do pentaminós É importante esclarecer que, para solução dos problemas, as peças podem ser giradas em todos os sentidos. Os problemas resumem-se na construção de formas geométricas, com a utilização de algumas ou todas as peças do jogo. Um problema interessante é o de se selecionar uma das peças, e com as demais (não há necessidade de se utilizar de todas) e reproduzi-la em escala maior. Existem outros inúmeros problemas possíveis, formar-se um retângulo ou um quadrado com as peças ou, ainda alguns animais:   Interessante notar-se que as soluções acima propostas não são as únicas para estes problemas. Considerando apenas as rotações múltiplas de 90 graus, obtemos as seguintes categorias de simetria: § L, N, P, F e Y podem ser orientados de 8 maneiras: 4 por rotação, e mais 4 pelo efeito de imagem espelho. § Z pode ser orientado de 4 maneiras: 2 por rotação, e 2 pelo efeito de imagem espelho. § T, V, U e W podem ser orientados em 4 maneiras através da rotação. § I pode ser orientado de duas maneiras através da rotação. § X pode ser orientado apenas de uma maneira. Esta atividade foi apresentada-me em um curso de Matemática, ofertado pela Unioeste. |
terça-feira, 6 de setembro de 2011
Assinar:
Postagens (Atom)